Scalable ML 笔记

lecture 3

线性回归模型 基本流程： - Obtain Raw Data - Split Data - Features Extraction - Supervised Learning - Evaluation - Predcit

经过清洗、提取特征，加上label，数据集被分成 训练集， 验证集， 测试集三部分。其中: - 算法在训练集上 学习，输出一个 模型。 - 模型中包含一些参数供调优。调优的参数构成一个调优空间。用训练集多次训练 ，遍历参数空间，在验证集上评估 模型的质量，得到一个参数最优的模型 - 用最优模型预测测试集。

线性回归模型输出一个 weight 向量，该向量有一个矩阵形式的 closing form:

$$ (X^TX)^-1*X^T$$

这里的 $X$ 是一个 $n*d$ 的矩阵， d 代表 特征向量的维度，n 代表 样本 x 的数量。 $ X^T $ 形如 $ [x1, x2, ... , x_n ] $

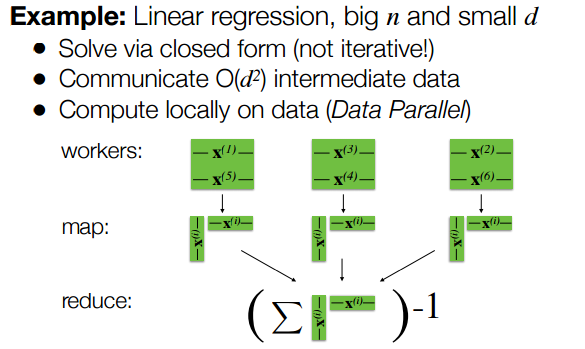
当样本量很大,而特征向量维度的较小的时候, 大矩阵相乘 可以转换成 矩阵的行向量外积之和。 利用spark的Mapreduce 过程，可以把 X的行向量分散到多个计算节点，在Map任务中 计算$ xi^T xi $, 在reduce 任务里对所有的 小矩阵求和，然后进行求逆运算。 用时间和空间复杂度来衡量，Map阶段 $ (X^TX) $ 的时间复杂度为 O$ nd^2) , 空间复杂度为 O$ d^2)； Reduce 阶段 $ Σ xi^T xi )^-1 $ 的时间复杂度为O$ d^3)， 空间复杂度为 $ O(d^2) $。

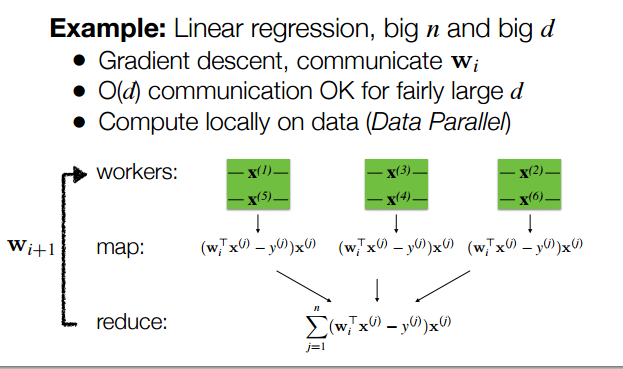
如果样本量很多，特征的维度也很多时，矩阵就会很大。 对于一个行和列都很大的矩阵，可以使用稀疏矩阵来加速计算，也可以通过各种数据清洗方法来减少特征数， 也可以使用梯度下降算法。 神奇的梯度下降算法，可以将Map 阶段的时间复杂度降低到 O$ nd), 空间复杂度变成 O$ d);

Reduce 阶段 的时间复杂度变成了 O$ d), 空间复杂度为 O$ d)

线性回归模型输出一个 weight 向量，该向量有一个矩阵形式的 closing form: $ X^TX)^-1X^T Y 这里的 X 是一个 n d 的矩阵， d 代表 特征向量的维度，n 代表 样本 x 的数量。 X^T 形如 \$ [x1, x2, ... , xn ])

当样本量很大,而特征向量维度的较小的时候, 大矩阵相乘 可以转换成 矩阵的行向量外积之和。 利用spark的Mapreduce 过程，可以把 X的行向量分散到多个计算节点，在Map任务中 计算 xi^T xi , 在reduce 任务里对所有的 小矩阵求和，然后进行求逆运算。 用时间和空间复杂度来衡量，Map阶段 $ X^TX) 的时间复杂度为 O$ nd^2) , 空间复杂度为O$ d^2)； Reduce 阶段 $ Σ xi^T xi )^-1 $ 的时间复杂度为O$ d^3)， 空间复杂度为 $ O(d^2) $ 。

如果样本量很多，特征的维度也很多时，矩阵就会很大。 对于一个行和列都很大的矩阵，可以使用稀疏矩阵来加速计算，也可以通过各种数据清洗方法来减少特征数， 也可以使用梯度下降算法。 神奇的梯度下降算法，可以将Map 阶段的时间复杂度降低到 O$ nd), 空间复杂度变成O$ d); Reduce 阶段 的时间复杂度变成了 O$ d), 空间复杂度为O$ d)

传输延迟对于算法设计的影响

数据传输速度不等式： 内存 > 硬盘 > 网络

设计算法的时候需要利用并行性，且意识到读写硬盘和网络会使程序速度变慢。

经验法则2：并行+ 内存计算 - 将数据留在内存，减少读写开销，尤其是在迭代计算时，如 梯度下降。 - Scale up（使用强大的多核机器）, 没有网络开销，硬件昂贵，不能无限扩容，最终会碰到瓶颈。 - Scale out （分布式，基于云计算的）：必须处理网络通讯，使用便宜的商用硬件，可以无限扩容

上图中，在开始迭代前，先执行 RDD.cache$ ) 使数据留在内存里，减少迭代时的硬盘读写。而这种写法，仍然会产生节点间的通讯。因为sum 函数是一个 action，它把节点间的数据收集起来，进行求和。

经验法则3：网络开销最小化 怎样减少网络通讯的开销？ 可以观察到，在ML 过程中我们需要存储并可能会传输 数据，模型和一些中间产物。 方案A: 使大对象本地化，设计合适的算法，确保大对象不会被传输。

下面贴两个例子，应对大N 小d 和 大N 大 d 的不同策略：